- cosinus
-
cosinus [ kɔsinys ] n. m. ♦ Fonction trigonométrique faisant correspondre à l'angle de deux axes la mesure de la projection orthogonale sur l'un, d'un vecteur unitaire porté par l'autre; sinus de l'angle complémentaire. Cosinus de l'angle θ(noté cos θ ).
● cosinus nom masculin (de co- et sinus) Cosinus de l'angle de couple de demi droites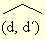
, réel de l'intervalle [-1, 1] égal au rapport de projection orthogonale de l'axe Δ′ sur l'axe Δ dans le plan euclidien, d et d′ étant les parties « positives » de Δ et Δ′. [On le note cos .]
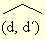Cosinus hyperbolique d'un réel x, réel noté ch x égal à 
.
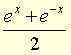Fonction cosinus, fonction définie sur R, qui, au réel x, associe le cosinus de l'angle dont x est la mesure modulo 2 π.
Cosinus phi (cos ϕ), expression mathématique du facteur de puissance d'un circuit parcouru par un courant alternatif sinusoïdal.
Fonction cosinus hyperbolique, fonction définie sur R : x ↦ ch x.
● cosinus (expressions)
nom masculin
(de co- et sinus)
Cosinus de l'angle de couple de demi droites 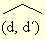, réel de l'intervalle [-1, 1] égal au rapport de projection orthogonale de l'axe Δ′ sur l'axe Δ dans le plan euclidien, d et d′ étant les parties « positives » de Δ et Δ′. [On le note cos .]
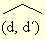Cosinus hyperbolique d'un réel x, réel noté ch x égal à .
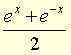Fonction cosinus, fonction définie sur R, qui, au réel x, associe le cosinus de l'angle dont x est la mesure modulo 2 π.
Cosinus phi (cos ϕ), expression mathématique du facteur de puissance d'un circuit parcouru par un courant alternatif sinusoïdal.
Fonction cosinus hyperbolique, fonction définie sur R : x ↦ ch x.
cosinusn. m. MATH Cosinus d'un angle aigu d'un triangle rectangle: rapport du côté adjacent à l'hypoténuse. V. trigonométrie. (Abrév.: cos).⇒COSINUS, subst. masc.Rapport entre la projection orthogonale d'un vecteur porté par un côté d'un angle sur l'autre côté, et ce vecteur. Abrév. cos. Le cosinus d'un angle est le sinus de son complément. Le cosinus de quarante-cinq degrés est égal au sinus (STENDHAL, Hist. peint. It., t. 1, 1817, p. 288). La dérivation de sinus x donne cosinus x (Gds courants pensée math., 1948, p. 287) :• ... Kirchhoff montre (...) que l'intensité du rayonnement émis dans une direction donnée doit être égal [sic] au produit de l'intensité émise normalement par le cosinus de l'angle formé par la normale avec la direction du rayonnement : c'est la « loi du cosinus » déduite en 1760 par Lambert de mesures expérimentales.Hist. Gén. des sc., t. 3, vol. 1, 1961, p. 291.Prononc. et Orth. :[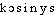
]. Pour s intervocalique prononcé 
] parce que le fait que le mot soit formé d'un rad. et d'un préf. n'est pas toujours ressenti. S final se prononce dans cactus, carolus, chorus, circus, coccus, cosinus (cf. KAMM. 1964, p. 199). Écrit co-sinus ds Ac. 1762, cf. aussi LAND 1834, GATTEL 1841 et BESCH. 1845. Admis sous la forme mod. ds Ac. 1835-1932. Étymol. et Hist. 1754 (Encyclop. t. 4). Dér. de sinus; préf. co-. Lat. sc. cosinus, 1620 (E. GUNTER [mathématicien angl. 1581-1626], Canon Triangulorum ds NED, s.v. cosine). Selon Encyclop. brit. et Lar. 19e, s.v. Gunter, c'est ce dernier qui a introduit le terme cosinus, à la place de sinus du complément. Fréq. abs. littér. :4.cosinus [kɔsinys; kosinys] n. m.ÉTYM. 1754; co-sinus, 1717; de co-, et sinus.❖♦ Math. Fonction faisant correspondre à l'angle de deux axes la mesure algébrique de la projection orthogonale sur l'un d'un vecteur unitaire porté par l'autre. || Le cosinus d'un angle est égal au sinus de l'angle complémentaire (⇒ Trigonométrie). || Des cosinus. || Fonction cosinus, qui à un nombre réel x fait correspondre le cosinus (noté cos x) de l'angle dont ce nombre est une mesure. — Cosinus hyperbolique.
Encyclopédie Universelle. 2012.
